Based on a
cognitive approach to visualizing dimensions,
this technology aims to expand the mind
and enable it to intuit and navigate four dimensional space.
This groundbreaking technology will answer questions like "What does a four dimensional cube really look like?" and "Can the human mind imagine four orthogonal directions?" apart from eventually opening up the world of four dimensional problem solving and even a four dimensional metaverse.
Studying the brain as it begins to understand four dimensions is a prospect at least as exciting as understanding 4D itself.
Our product is brain training technology designed to develop 4D vision.
The next few sections develop the theory behind our technology.
Emergence of a third dimension
Each animation above shows an animated quadrilateral. In the first, the vertices of the quadrilateral oscillate in an uncorrelated manner, while in the second, they move like the corners of a rectangle rotating in 3D space, projected onto a 2D screen.
The sides of the quadrilaterals in both animations continuously change length.
Cover one eye to eliminate the stereoscopic effect, and watch each animation.
Even when viewed with one eye, the Rotation + Projection animation is instantly recognizable as an object in 3D space. The shape appears rigid, for which the brain has to invent a 3D space.
The Rotation + Projection animation in this demo shows how 2D images can give rise to 3D vision.
Our technology operates on the same underlying mechanism.
Rotation is the key
Our understanding identifies rotating objects as the key to developing vision.
Rotation provides dense and structured information about the rotating object
and the space it occupies.
Consider the following narrative of a baby learning 3D vision
- 3D Object
Our baby's object is a crib mobile. A crib mobile is a colorful spinning toy usually suspended over an infant's crib.
- Rotation
The baby's crib mobile spins and holds the baby's attention.
- Projection
Our eyes can be thought of as 2D sensors that take in 2D projections of our 3D world.
Without developed 3D vision or depth perception, the baby views its revolving crib mobile as a continuous stream of flat warping images. Its toy looks different from different angles, and since the toy is rotating through different angles, it appears to change shape as it turns.
- Knitting
As the baby's brain tries to make sense of these warping images, it begins to stitch together the 2D perspective projections of 3D objects.
The baby with the spinning crib mobile as with other objects begins to see that the turning object is not warping, but simply being viewed from different perspectives.
- Vision
What does it mean to 'see' 3D, or have 3D vision?
Recognizing 3D space as continuous, the ability to determine which points are close to one another, and which are far apart, the ability to determine which points are which direction from one another, and the resulting ability to navigate within space, all combine to let us see that space.
The baby's developing intuition allows it to recognize its toy from various perspectives, manipulate its toy, and successfully place its toy in its mouth.
Now we mimic the conditions that led to the baby developing 3D vision, but do so in 4D space
- 4D object
Our 4D objects are virtual.
We build virtual 4D objects by embedding points in 4D space. A point's location in 4D space is represented by a point vector (x, y, z, w). Points in turn are represented by tiny 4D spheres.
So our 4D objects are point clouds made up of thousands of points arranged in geometrical patterns to form shapes.
- Rotation
To rotate objects in 4D space we built a generic and intuitive representation for rotations shown in the essential math section below.
Rotations in 4 dimensional space have 6 degrees of freedom - around the xy, xz, xw, yz, yw, and zw planes (rotations in 3D space have only 3 degrees of freedom - around the xy, xz, and yz planes)
As the object rotates, the distance between any two points in the point cloud object remains the same.
- Projection
We project the 4D object onto a 3D screen, which can be rendered on a VR headset.
The same way the baby saw warping 2D projections of his rotating 3D toy, our technology will show you warping 3D projections of a 4D object.
It is important to remember that in both the 3D and 4D case, the object doesn't actually warp, only its projection warps as the object rotates through a range of angles.
- Knitting
Since the 4D object is a rigid body rotating, and the object is continuously being projected as it rotates, its projection causes a predictable warping that our brains can learn to ignore.
Instead of seeing warping, the stream of images becomes recognizable as a rigid object rotating in 4D space.
- Vision
Learning the 4D object through rotation gives us insights into 4D space so that we begin to intuit and 'see' 4D.
What does it mean to 'see' 4D? Recognizing 4D space as continuous, the ability to determine which points are close to one another, and which are far apart, the ability to determine which points are which direction from one another, and the resulting ability to navigate 4D space, all combine to let us see 4D objects in 4D space.
How we do it

5
View
rendered animation to develop4D intuition
Try it out!
Neural Net Analogy
A conceptual model for the brain's vision algorithm
This is a simplified look at a tiny section of the brain's function if it worked as a network of neural nets.
When the brain is fed 'LIGHT IN' input that corresponds to rotating 3D objects, the brain develops 3D vision. We hypothesize that some area of the middle layers correspond to 2D vision, which is then further processed into 3D vision.
We then employ a transfer learning sort of approach which is built upon our brain's mature 3D vision algorithm, to process the incoming 3D projections as existing in coherent 4D space.
The parallel to a loss function (that drives the learning) in this example would be how well we're able to navigate the world. This includes things like successfully grabbing and recognizing a toy, manipulating objects, dodging a swinging branch, or climbing a tree. These incentivize and reinforce the mechanism that generates 3D vision in our minds from the input it receives.
A loss function for 4D space, would be the ability to navigate the space. This includes things like recognizing objects from different angles, recognizing different types of rotations, manipulating objects and more.
Essential Math
Rotations
To view an object from all angles, we employ continuous rotations, thus mastering rotations in 4 dimensions is core to our technology.
Rotations are continuous linear transformations that preserve shapes by preserving distance between points, or equivalently, preserving lengths of vectors in space.
For a rotation R acting on any vector v, (Rv)2 = v2 or, in matrix form, vTRTRv = vTv, leading to the characterization
RTR = I
Every rotation is equivalant to a sequence of infinitesimal (tiny) rotations. We can construct arbitrary rotations if we know the form of an arbitrary infinitesimal rotation. We seek such a rotation in the form
R = I + m
where m is an infinitesimal matrix (measuring the departure of R from the identity matrix I) constrained by
I = RTR = (I + m)T(I + m)
= I + m + mT + mTm
Dropping mTm (second order infinitesimal)
m + mT = 0 or mT = -m
Thus, an infinitesimal rotation matrix is the identity matrix + an infinitesimal antisymmetric matrix.
Such a rotation in 4 dimensions has the explicit matrix form
| 1 | a | b | c |
| -a | 1 | d | e |
| -b | -d | 1 | f |
| -c | -e | -f | 1 |
characterized by 6 independent, infinitesimal parameters (a...f).
Perspective Projection
The 4D space (xyzw) is projected onto a 3D screen (the xyz hyperplane) from the perspective of an eye placed at ŵ (the unit vector in w direction)
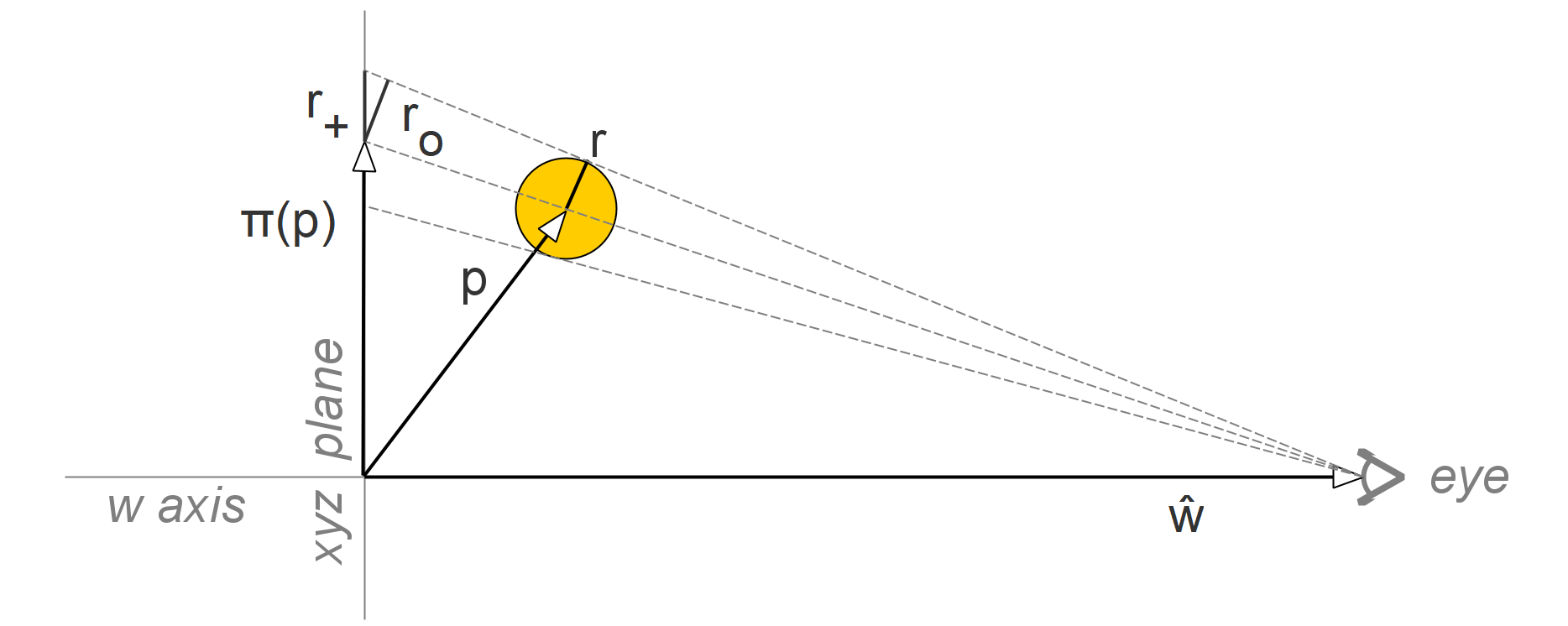
The point at p projects onto π(p).
1 - p⋅ŵ
A tiny sphere of radius r placed at p will project to an ellipsoid with its longest radius r+ parallel to π(p) and the shortest radii ro (all) perpendicular to π(p).
1 - p⋅ŵ
r+ = √1 + π(p)2 ro